sigma-se

目的

この記事では、偏微分と勾配についての簡単な実装サンプルを記載する。

概念の説明と実装サンプル

偏微分のおさらい

大まかに言うと偏微分は、微分対象（変数）が複数になる場合の微分のことだが、数式で表現すると少し長くなるため、微分対象が2つ（$x_{0} と x_{1}$）で、$x_{0}$ で偏微分する場合を例にした以下の定義にとどめる。

\[ f_{x_{0}}(x_{0}, x_{1}) = ∂_{x_{0}}(x_{0}, x_{1}) = \frac{∂\ (x_{0}, x_{1})}{∂x_{0}} \]

\[ = \lim_{\Delta x_{0} \to 0} \frac{ f(x_{0}+\Delta x_{0}, x_{1}) - f(x_{0}, x_{1}) }{\Delta x_{0}} \]

$f_{x_{0}}(x_{0}, x_{1})$、$∂_{x_{0}}(x_{0}, x_{1})$、$\frac{∂\ (x_{0}, x_{1})}{∂x_{0}}$ は、$f(x)$ を $x_{0}$ で偏微分した結果（偏導関数）を表す記号。
微分の定義については、前ページを参考のこと Python - AI : 損失関数と数値微分（勾配）の実装サンプル > 微分のおさらい

偏微分のPython実装サンプル

以下、$f(x_{0}, x_{1}) = x^2_{0} + x^2_{1}$ を例に偏微分のPython実装サンプルを解説する。

最初に、グラフ $f(x_{0}, x_{1}) = x^2_{0} + x^2_{1}$

$ python
    >>> from mpl_toolkits.mplot3d import Axes3D
    >>> import matplotlib.pyplot as plt
    >>> import numpy as np
    >>>
    >>> def func_ex(x0, x1):
    ...     return x0**2 + x1**2
    ...
    >>> x = np.arange(-3.0, 3.0, 0.1)
    >>> x0 = np.arange(-3.0, 3.0, 0.1)
    >>> x1 = np.arange(-3.0, 3.0, 0.1)
    >>> X0, X1 = np.meshgrid(x0, x1)
    >>> Z = func_ex(X0, X1)
    >>> fig = plt.figure()
    >>> ax = Axes3D(fig)
    >>> ax.set_xlabel("x0")
    Text(0.5, 0, 'x0')
    >>> ax.set_ylabel("x1")
    Text(0.5, 0, 'x1')
    >>> ax.set_zlabel("f(x0, x1)")
    Text(0.5, 0, 'f(x0, x1)')
    >>> ax.set_title("f(x0, x1) = x0^2+x1^2 # arange:-3.0, 3.0, 0.1, label:f(x0, x1), x0, x1")
    Text(0.5, 0.92, 'f(x0, x1) = x0^2+x1^2 # arange:-3.0, 3.0, 0.1, label:f(x0, x_{1}), x0, x_{1}')
    >>> ax.plot_wireframe(X0, X1, Z)
    [<mpl_toolkits.mplot3d.art3d.Line3DCollection object at 0x7f6ae0cec6d8>]
    >>> plt.savefig('/static/tblog/img/pid25_1.png')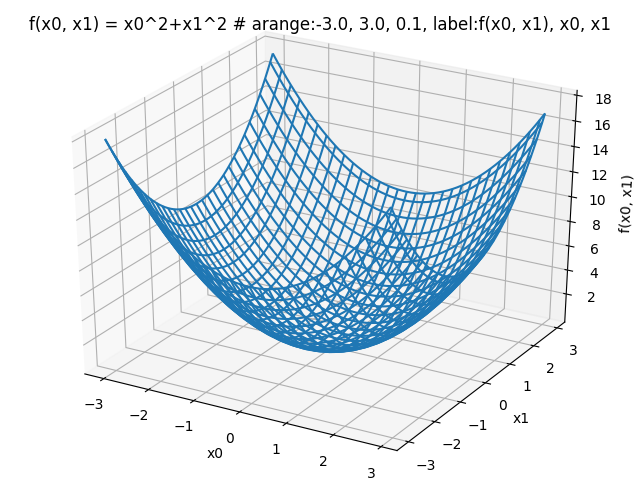
    >>>

pid25_1

次に偏微分のPython実装サンプル
まず、どの変数に対して偏微分するか前提が必要となる。

例えば、関数 $f(x_{0}, x_{1}) = x^2_{0} + x^2_{1}$ で $x_{0} = 5$、$x_{1} = 10$ とした時

$x_{0}$ に対する偏微分を求めるには、まず $x_{1}$ に対して解析的な微分（真の微分：$y = x^{n}$⇒$y’ = nx^{n-1}$）を行う。

$x^2_{0} + x^2_{1}$ を $x_{1}$ で解析的な微分をすると

\[ x^2_{0} + 2x_{1}\hspace{5mm}･･･（A） \]
と表せる。

ここで偏微分の対象は、$x_{0}$ なので、$（A）$ を $x_{1} = 10$ とし

\[ x^2_{0} + 2\times10\hspace{5mm}･･･（B） \]

と表せ、この$（B）$を $x_{0}$ で偏微分することになる。

$（B）$は、下記サンプル func_partial_difと表せるため、これに対して $x_{0} = 5.0$ で数値微分する形で偏微分を求めることができる。
```
$ python
    >>> def num_dif(f, x):    # 下記（＊ num_dif）参照
    ...     h = 1e-4
    ...     return (f(x+h) - f(x-h)) / (2 * h)
    ...
    >>> def func_partial_dif(x0):
    ...     return x0*x0 + 2.0**10.0
    ...
    >>> num_dif(func_partial_dif, 5.0)
    9.999999999976694
    >>>
```
※ num_dif（数値微分）については、 Python - AI : 損失関数と数値微分（勾配）の実装サンプル > 数値微分の関数定義（Python実装サンプル）を参考のこと。
次項の解説ため $x_{1}$ に対する偏微分の方も求めておく
$x_{0}$ で解析的微分をすると

\[ 2x_{0} + x^2_{1}\hspace{5mm}･･･（C） \]

と表せ、偏微分の対象は、$x_{1}$ なので、この$（C）$を $x_{0} = 5$ とした

\[ 2*5 + x^2_{1}\hspace{5mm}･･･（D） \]

を $x_{1}$ で偏微分する。
```
$ python
    >>> def num_dif(f, x):
    ...     h = 1e-4
    ...     return (f(x+h) - f(x-h)) / (2 * h)
    ...
    >>> def func_partial_dif(x1):
    ...     return 2.0**5.0 + x1*x1
    ...
    >>> num_dif(func_partial_dif, 10.0)
    19.99999999995339
    >>>
```
※ 結局、偏微分と言っても、微分対象となる変数以外をすべて固定値と捉えて微分しているに過ぎない。

勾配のPython実装サンプル

上記で、$x_{0}$、$x_{1}$ それぞれの偏微分について実装サンプルを解説したが、次は、同時に偏微分する場合を考える。

$x_{0}$、$x_{1}$ 両方の偏微分 $\displaystyle \left(\frac{∂\ (x_{0}, x_{1})}{∂x_{0}}, \frac{∂\ (x_{0}, x_{1})}{∂x_{1}} \right)$ をベクトルとしてまとめたものを勾配という。

勾配の実装サンプル
※ 微分、偏微分の概念や説明については、既に説明済なので割愛。

$ python
    >>> import numpy as np
    >>>
    >>> def func_ex(x):    # このページで使用しているサンプル関数の定義
    ...     return x[0]**2 + x[1]**2
    ...
    >>> def num_gradient(f,x):    # 勾配関数
    ...     h = 1e-4
    ...     grad = np.zeros_like(x)    # xと同じ形状の配列で値がすべて 0
    ...
    ...     for idx in range(x.size):    # x の次元分ループする。 (下記例は、5.0, 10.0 の 2 周ループ)
    ...         idx_val = x[idx]
    ...         x[idx] = idx_val + h
    ...         fxh1 = f(x)    # f(x + h)の算出
    ...
    ...         x[idx] = idx_val - h
    ...         fxh2 = f(x)    # f(x - h)の算出
    ...
    ...         grad[idx] = (fxh1 - fxh2) / (2 * h)
    ...         x[idx] = idx_val    # 値をループ先頭の状態に戻す。
    ...     return grad
    ...
    >>>

勾配関数の実施確認
この勾配関数で前項の $x_{0} = 5$、$x_{1} = 10$ とした時をはじめ、いくつかの点の勾配を出してみる。
```
$ python
    >>> num_gradient(func_ex, np.array([5.0, 10.0]))
    array([10., 20.])
    >>> num_gradient(func_ex, np.array([0.0, 10.0]))
    array([ 0., 20.])
    >>> num_gradient(func_ex, np.array([5.0, 0.0]))
    array([10.,  0.])
    >>> num_gradient(func_ex, np.array([2.0, -4.0]))
    array([4., -8.])
    >>> num_gradient(func_ex, np.array([-3.0, 4.0]))
    array([-6., 8.])
    >>>
```
上記の勾配はすべて、解析的な微分（真の微分）$y = x^{n}$⇒$y’ = nx^{n-1}$ となる $(2x_{0} , 2x_{1})$ になっていることがわかる。

それぞれの勾配を見てみると

$(5.0,\ 10.0)$ ⇒ $(10.0,\ 20.0)$
$(0.0,\ 10.0)$ ⇒ $(0.0,\ 20.0)$
$(5.0,\ 0.0)$ ⇒ $(10.0,\ 0.0)$
$(2.0,\ -4.0)$ ⇒ $(4.0,\ -8.0)$
$(-3.0,\ 4.0)$ ⇒ $(-6.0,\ 8.0)$

となっており、ベクトルを逆にした勾配を見ると

$(10.0,\ 20.0)$ ⇒ $(5.0,\ 10.0)$
$(0.0,\ 20.0)$ ⇒ $(0.0,\ 10.0)$
$(10.0,\ 0.0)$ ⇒ $(5.0,\ 0.0)$
$(4.0,\ -8.0)$ ⇒ $(2.0,\ -4.0)$
$(-6.0,\ 8.0)$ ⇒ $(-3.0,\ 4.0)$

となり、すべて原点 $0$ の方向にベクトルが向いていることがわかる。

この勾配は、原点 $0$ から遠くなればなるほどベクトルが大きく（長さ）なっており、それぞれの場所において、この関数がどれだけ最小値（この記事に例では $0$）から離れているか、大きさや方向を示している。

参考文献

斎藤康毅（2018）『ゼロから作るDeep Learning - Pythonで学ぶディープラーニングの理論と実装』株式会社オライリー・ジャパン

SIGMA-SE Tech Blog