目的

この記事では、多層パーセプトロンの概念と簡単な実装サンプルについて記載する。

概念の説明と実装サンプル

単純パーセプトロンの限界

前の記事 で単純パーセプトロンをAND、NAND、OR の論理回路で実装できることを説明したが、排他的論理和と呼ばれる下記XORゲートになると、以下で示す非線形でしか \(0\) と \(1\) の領域を分けられない。
（単純パーセプトロンは、線形（直線）でしか \(0\) と \(1\) の領域を分けられない。）

• XORゲートの真理値表

  \(x_{1}\)	\(x_{2}\)	\(y\)
  0	0	0
  1	0	1
  0	1	1
  1	1	0

  下記の入力値が2つあるパーセプトロン\(（A）\)に対して、ORゲートを満たす、パラメータ \((b, w_{1}, w_{2}) = (-0.5, 1.0, 1.0)\) を与えた場合を例にその根拠を説明する。

  \[ {\small y = \begin{cases} 0 \hspace{5pt}\text{if}\hspace{5pt}b + x_{1}w_{1} + x_{2}w_{2} \leqq 0 \\ 1 \hspace{5pt}\text{if}\hspace{5pt}b + x_{1}w_{1} + x_{2}w_{2} > 0 \end{cases}\hspace{5mm}･･･（A） } \]

  パラメータ \((b, w_{1}, w_{2}) = (-0.5, 1.0, 1.0)\) を指定すると

  \[ {\small y = \begin{cases} 0 \hspace{5pt}\text{if}\hspace{5pt}-0.5 + x_{1} + x_{2} \leqq 0 \\ 1 \hspace{5pt}\text{if}\hspace{5pt}-0.5 + x_{1} + x_{2} > 0 \end{cases}\hspace{5mm}･･･（B） } \]

  よって、上記\(（B）\)の境界線は

  \[ {\small -0.5 + x_{1} + x_{2} = 0\hspace{5mm}･･･（C） } \]

  となるため、下記グラフが境界線となる。

  

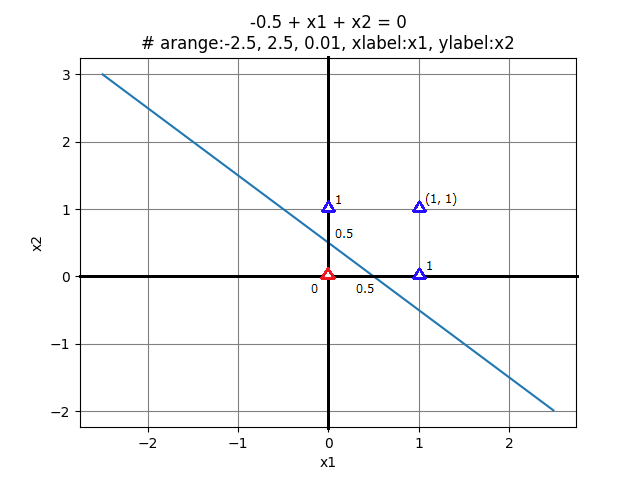
  そして、グラフ上の4つの点「△」は、下記ORゲートの真理値表で \(y = 0\) となる △ と \(y = 1\) となる △ を表している。

  \(x_{1}\)	\(x_{2}\)	\(y\)
  0	0	0
  1	0	1
  0	1	1
  1	1	1

  このように\(（B）\) は、 \(0\) と \(1\) の領域を線形（直線）で分けることができる。
  一方、冒頭で触れたXORゲートになると、上記XORゲートの真理値表の通り、\((x_{1}, x_{2}) = (1, 1)\) の時、\(y=0\) となるため、 下記グラフの △ と △ で領域を分けているように、非線形でしか分けることができない。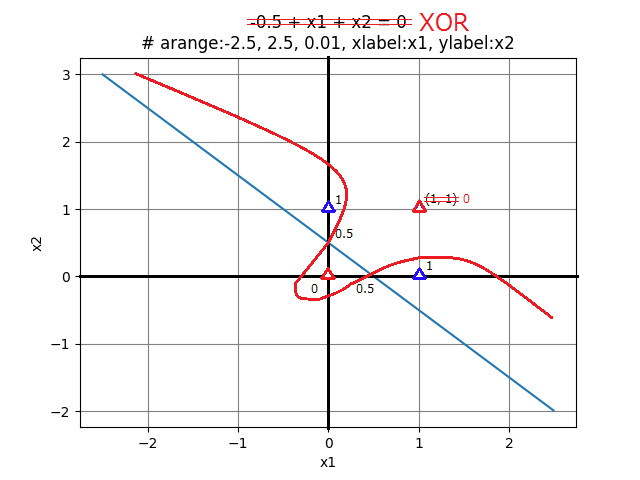

  

多層パーセプトロンの概念

上記で触れたの通り、単純パーセプトロン（入力層と出力層のみの2層）では、XORゲートを表現できないが多層パーセプトロン（入力層が多層）だとそれが可能になる。

単純パーセプトロンの説明で触れてきたAND、NAND、ORゲートを下記 1. ～ 3. で組み合わせれば、4. XORゲートの真理値表の通り、多層パーセプトロンを表現できる。

• 1. NANDゲート

  \[ {\small s_{1} = \begin{cases} 0 \hspace{5pt}\text{if}\hspace{5pt}b + x_{1}w_{1} + x_{2}w_{2} \leqq 0 \\ 1 \hspace{5pt}\text{if}\hspace{5pt}b + x_{1}w_{1} + x_{2}w_{2} > 0 \end{cases} } \]

• 2. ORゲート

  \[ {\small s_{2} = \begin{cases} 0 \hspace{5pt}\text{if}\hspace{5pt}b + x_{1}w_{1} + x_{2}w_{2} \leqq 0 \\ 1 \hspace{5pt}\text{if}\hspace{5pt}b + x_{1}w_{1} + x_{2}w_{2} > 0 \end{cases} } \]

• 3. ANDゲート

  \[ {\small y = \begin{cases} 0 \hspace{5pt}\text{if}\hspace{5pt}b + s_{1}w_{1} + s_{2}w_{2} \leqq 0 \\ 1 \hspace{5pt}\text{if}\hspace{5pt}b + s_{1}w_{1} + s_{2}w_{2} > 0 \end{cases} } \]

• 4. XORゲートの真理値表
  上記 1. ～ 3. の単純パーセプトロンを左辺 \(s_{1}\), \(s_{2}\), \(y\) で結合すると、下記 XORゲートの真理値表として表現することができる。

  \(x_{1}\)	\(x_{2}\)	\(s_{1}\)	\(s_{2}\)	\(y\)
  入力値1	入力値2	1. の出力	2. の出力	3. の出力
  0	0	1	0	0
  1	0	1	1	1
  0	1	1	1	1
  1	1	0	1	0

  • 補足
    • 入力値1（\(x_{1}\)）、入力値2（\(x_{2}\)）のNANDゲートが 1. の出力（\(s_{1}\)）となる。
    • 入力値1（\(x_{1}\)）、入力値2（\(x_{2}\)）のORゲートが 2. の出力（\(s_{2}\)）となる。
    • 1.の出力（\(s_{1}\)）、2.の出力（\(s_{2}\)）のANDゲートが 3. の出力（\(y\)）となる。

多層パーセプトロンの実装サンプル

最後に実装サンプル。

• AND、NAND、ORゲートを定義
  前の記事 > 単純パーセプトロンの実装サンプル で触れているANDゲートに加え、パラメータ \(w_{1}\)（重み1）, \(w_{2}\)（重み2）, \(b\)（バイアス）をNANDゲート、ORゲートの真理値表を満たすように変え、以下のように定義する。

  $ python
  >>> import numpy as np
  >>> def AND(x1, x2):    # （＊1）ANDゲートの定義
  ...     x = np.array([x1, x2])    # 入力
  ...     w = np.array([0.5, 0.5])    # 重み
  ...     b = -0.7    # バイアス
  ...     tmp = np.sum(w*x) + b
  ...     if tmp <= 0:
  ...         return 0
  ...     else:
  ...         return 1
  ...
  >>> def NAND(x1, x2):    # （＊2）NANDゲートの定義
  ...     x = np.array([x1, x2])    # 入力
  ...     w = np.array([-0.5, -0.5])    # 重み
  ...     b = 0.7    # バイアス
  ...     tmp = np.sum(w*x) + b
  ...     if tmp <= 0:
  ...         return 0
  ...     else:
  ...         return 1
  ...
  >>> def OR(x1, x2):    # （＊3）ORゲートの定義
  ...     x = np.array([x1, x2])    # 入力
  ...     w = np.array([0.5, 0.5])    # 重み
  ...     b = -0.2    # バイアス
  ...     tmp = np.sum(w*x) + b
  ...     if tmp <= 0:
  ...         return 0
  ...     else:
  ...         return 1
  ...
  

  あとは、上記（＊1）～（＊3）それぞれの引数と戻り値を上記XORゲートの真理値表に合わせて実装するだけ。

• XORゲートの実装サンプル

  >>> def XOR(x1, x2):    # XORゲートの定義
  ...     s1 = NAND(x1, x2)
  ...     s2 = OR(x1, x2)
  ...     y = AND(s1, s2)
  ...     return y
  ...
  >>> XOR(0, 0)    # （＊4） 0 を出力
  0
  >>> XOR(1, 0)    # （＊5） 1 を出力
  1
  >>> XOR(0, 1)    # （＊6） 1 を出力
  1
  >>> XOR(1, 1)    # （＊7） 0 を出力
  0
  

  上記（＊4）～（＊7）の通り、XORゲートが実装できた。
  （XORゲートの真理値表の \(y\) が出力できている。）