目的

この記事では、ニューラルネットワークの活性化関数と実装サンプルについて記載する。

※ 活性化関数は、パーセプトロンの原理を基にしてニューラルネットワークを理解するための架け橋的な役割を持つ。

概念の説明と実装サンプル

パーセプトロンと活性化関数

活性化関数（activation function）は、伝達関数（transfer function）とも呼ばれ、入力値の総和を出力に変換する関数のことを言い、入力値がどのように発火するか（活性化するか・伝達されるか）を決定する役割を持つ。

前の記事 > 多層パーセプトロンの概念と実装サンプル で触れた入力値が2つあるパーセプトロン\(（A）\)も活性化関数と言えるが、一般的な活性化関数の表現に書き換えると右辺を \(a = b + x_{1}w_{1} + x_{2}w_{2} \) と置き、\(（B）\) 、\(y\) を \(h(a)\) で表現した\(（C）\)のように表せる。

\(a = b + x_{1}w_{1} + x_{2}w_{2} \) と置き

\(y\) = \(h(a)\) とすると

となり、入力値の総和を \(h(a)\) によって変換し、出力値である \(y\) となることを表わしている。

※ \(（C）\) のイメージ

　

上記の \(a\)、\(h(x)\)、\(y\) の 〇 を ニューロン（またはノード）と呼ぶ。

上記の通り、\(（C）\)で表される活性化関数は、バイアスを境に出力が切り替わる関数となっているが、このような関数をステップ関数または、階段関数という。

従ってパーセプトロンは、活性化関数に分類されるステップ関数を用いて表現されてる。

この活性化関数は、ステップ関数ではなく、次項で触れるシグモイト関数を用いることで、自動学習が可能なニューラルネットワークを表現できるようになる。

※ 単純/多層パーセプトロンでは、意図した論理回路が実現するように適切な \(w\)（重み）を人力で判断しなければならなかったが、ニューラルネットワークでは、その判断を自動学習できるようになる。

ニューラルネットワークと活性化関数（シグモイド関数）

ニューラルネットワークで使用される活性化関数の一つにシグモイド関数（sigmoid function）がある。

前項で触れたパーセプトロンもニューラルネットワークも入力値を関数で変換し出力してるが、 その違いは、ステップ関数であるかシグモイド関数であるかだけの違い。

ここで深く掘り下げないが一般的なシグモイド関数は、下記\(（D）\)で表される実関数を指している。

\(a\) は、ゲイン（増幅値）と呼ばれ、\(a = 1\) とした下記\(（E）\)は、神経細胞が持つ性質をモデル化したものとして用いられており、標準シグモイド関数という。

※ \(e=2.718281828…\) は、無理数で自然対数の低を表し、ネイピア数という。

以降、ステップ関数とシグモイド関数の実装サンプルとその違いについて記載する。

ステップ関数の実装サンプル

下記（＊1）は、\(x>0\) を基準にそれが真であれば、\(1\)、そうでなければ \(0\) を出力するステップ関数の実装サンプル。

$ python
 >>> import numpy as np
 >>> def step_func(x):    # （＊1） ステップ関数の定義
 ...     y = x > 0
 ...     return y.astype(np.int)
 ...

上記引数の \(x\) を（＊2）のNumPy配列で定義する。

$ python
 >>> x = np.array([-0.5, 0.5, 1.5])    # （＊2） NumPy配列の定義
 >>> x    # （＊3）NumPy配列の確認
 array([-0.5,  0.5,  1.5])

ここで（＊4）の通り、\(x\) を \(x > 0\) とするとbool値のNumPy配列が返さる。

$ python
 >>> x > 0    # （＊4） NumPy配列をbool値で表示
 array([False,  True,  True])

さらに（＊5）でこの \(x > 0\) をastypeでint変換している。

$ python
 >>> (x > 0).astype(np.int)    # （＊5） NumPy配列のbool値を 0：false、1：true で表示
 array([0, 1, 1])
 >>>

よって、（＊2）の引数 \(x = [-0.5, 0.5, 1.5]\) が戻り値となる（＊5）のNumPy配列が \(x = [0, 1, 1]\) で出力されている。
さらに、（＊1）を numpy.array の表現に書き換えると（＊6）のように \(1\) STEPで表現することができる。

$ python
 >>> import numpy as np
 >>> import matplotlib.pylab as plt
 >>> def step_func(x):    # （＊6） ステップ関数の定義
 ...    return np.array(x > 0, dtype=np.int)
 ...

上記（＊6）のグラフ出力

 >>> x = np.arange(-5.0, 5.0, 0.1)    # 区間を-5～5 まで、描画制度を 0.1 刻みに設定
 >>> y = step_func(x)    # （＊6） ステップ関数をコール
 >>> plt.title("step_func\n# arange:-5.0, 5.0, 0.1, xlabel:x, ylabel:y")    # グラフタイトルを設定
 Text(0.5, 1.0, 'step_func\n# arange:-5.0, 5.0, 0.1, xlabel:x, ylabel:y')
 >>> plt.ylim(-0.1, 1.1)    # y軸の範囲を設定
 (-0.1, 1.1)
 >>> plt.xlabel("x")    # x軸のラベルを設定
 Text(0.5, 0, 'x')
 >>> plt.ylabel("y")    # y軸のラベルを設定
 Text(0, 0.5, 'y')
 >>> plt.plot(x, y)    # グラフの描画
 [<matplotlib.lines.Line2D object at 0x7f7e0a48e2b0>]
 >>> plt.savefig('/var/www/vops/ops/macuos/static/macuos/img/b_id40_2.png')    # グラフの出力

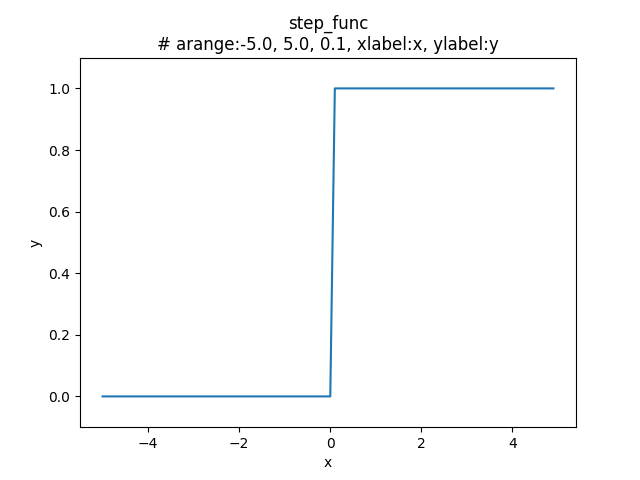
上記グラフの通り \(x = 0\) を境に \(y\) が \(0\) から \(1\) に切り替わっており、階段状になっていることからステップ関数は、階段関数とも呼ばれている。

シグモイド関数の実装サンプル

上記、シグモイド関数\(（E）\)の \(e^{-x}\) をNumPyで書き換えるだけで良く、下記 \(1\) STEPのみ。

$ python
 >>> import numpy as np
 >>> import matplotlib.pylab as plt
 >>> def sigmoid_func(x):    # （＊7） シグモイド関数の定義
 ...     return 1 / (1 + np.exp(-x))    # 自然対数の低 (e) の -x 乗
 ...

引数に関しては、ステップ関数と同様にNumPy配列を渡すとNumPy配列で出力される。

 >>> x = np.array([-3.0, -2.0, -1.0, 0, 1.0, 2.0, 3.0])
 >>> sigmoid_func(x)
 array([0.04742587, 0.11920292, 0.26894142, 0.5, 0.73105858, 0.88079708, 0.95257413])
 >>>

上記（＊7）のグラフ出力

 >>> x = np.arange(-5.0, 5.0, 0.1)    # 区間を-5～5 まで、描画制度を 0.1 刻みに設定
 >>> y = sigmoid_func(x)    # （＊7） シグモイド関数をコール
 >>> plt.title("sigmoid_func\n# arange:-5.0, 5.0, 0.1, xlabel:x, ylabel:y")    # グラフタイトルを設定
 Text(0.5, 1.0, 'sigmoid_func\n# arange:-5.0, 5.0, 0.1, xlabel:x, ylabel:y')
 >>> plt.ylim(-0.1, 1.1)    # y軸の範囲を設定
 (-0.1, 1.1)
 >>> plt.xlabel("x")    # x軸のラベルを設定
 Text(0.5, 0, 'x')
 >>> plt.ylabel("y")    # y軸のラベルを設定
 Text(0, 0.5, 'y')
 >>> plt.plot(x, y)
 [<matplotlib.lines.Line2D object at 0x7ff62b64fcf8>]
 >>> plt.savefig('/var/www/vops/ops/macuos/static/macuos/img/b_id40_3.png')    # グラフの出力

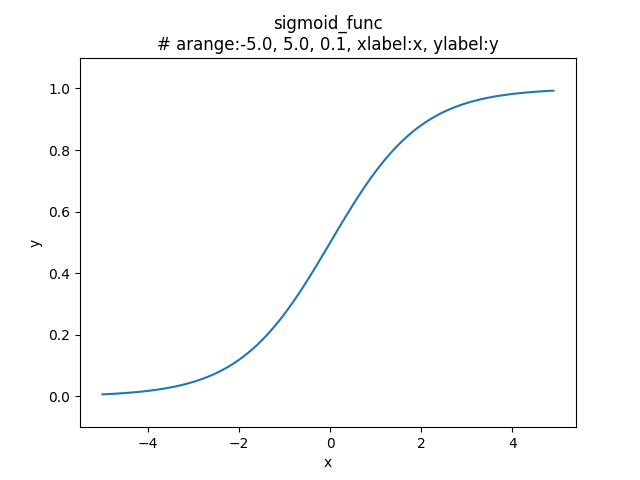
ステップ関数とシグモイド関数の違い

ステップ関数は、\(y = 0\) or \(y = 1\) のみの出力なのに対してシグモイド関数の出力 \(y\) は、連続的な実数を出力しており、滑らかな曲線を描いている。

これは、ニューラルネットワークのシグモイド関数がパーセプトロンのステップ関数では表現できない柔軟性や複雑な処理を表現できることを意味し、自動学習においても重要な役割を果たしている。

参考文献

• 斎藤 康毅（2018）『ゼロから作るDeep Learning - Pythonで学ぶディープラーニングの理論と実装』株式会社オライリー・ジャパン