目的
この記事では、活性化関数であるステップ、シグモイド、ReLU、恒等関数、ソフトマックス関数関数の実装サンプルについて記載する。
概念の説明と実装サンプル
ステップ関数
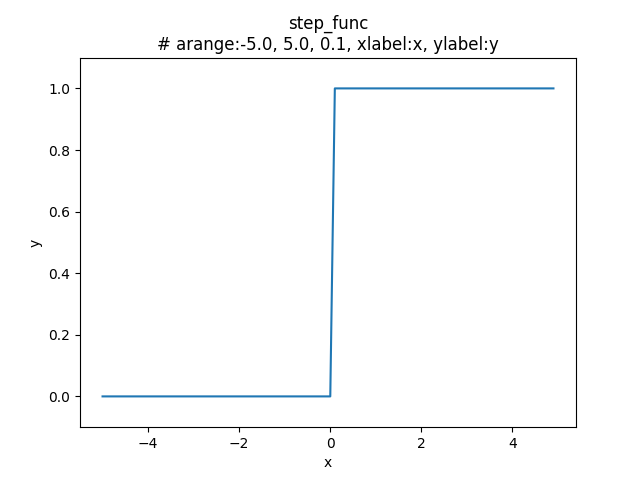
前の記事 > ニューラルネットワークの活性化関数と実装サンプル で触れたステップ関数で、線形の活性化関数であり階段関数とも呼ばれる。
- 定義
\(x\) が \(0\) より大きければ、\(1\) を出力し、\(0\) 以下であれば \(0\) を出力する。
\[
{\normalsize
h(x) =
\begin{cases}
0 \hspace{5pt}\text{if}\hspace{5pt}x \leqq 0 \\
1 \hspace{5pt}\text{if}\hspace{5pt}x > 0
\end{cases}
}
\]
- 実装
$ python
>>> import numpy as np
>>> import matplotlib.pylab as plt
>>> def step_func(x): # ステップ関数の定義
... return np.array(x > 0, dtype=np.int)
...
- グラフ出力
$ python
>>> x = np.arange(-5.0, 5.0, 0.1) # 区間を-5~5 まで、描画制度を 0.1 刻みに設定
>>> y = step_func(x) # ステップ関数をコール
>>> plt.title("step_func\n# arange:-5.0, 5.0, 0.1, xlabel:x, ylabel:y") # グラフタイトルを設定
Text(0.5, 1.0, 'step_func\n# arange:-5.0, 5.0, 0.1, xlabel:x, ylabel:y')
>>> plt.ylim(-0.1, 1.1) # y軸の範囲を設定
(-0.1, 1.1)
>>> plt.xlabel("x") # x軸のラベルを設定
Text(0.5, 0, 'x')
>>> plt.ylabel("y") # y軸のラベルを設定
Text(0, 0.5, 'y')
>>> plt.plot(x, y) # グラフの描画
[<matplotlib.lines.Line2D object at 0x7fc13041e278>]
>>> plt.savefig('/var/www/vops/ops/macuos/static/macuos/img/pid18_1.png')) # グラフの出力
シグモイド関数
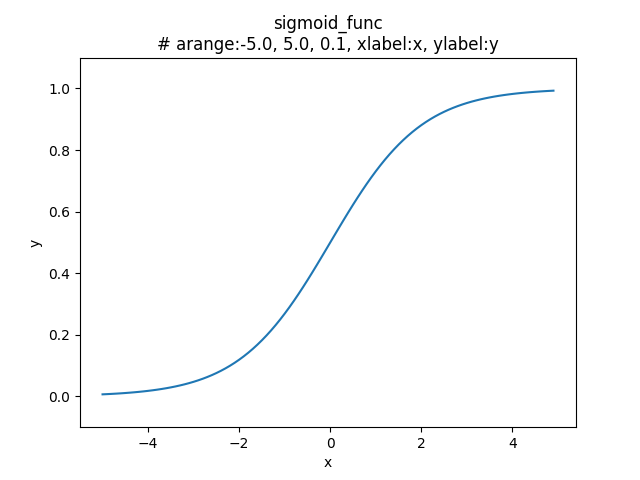
前の記事 > ニューラルネットワークの活性化関数と実装サンプル で触れたシグモイド関数で、非線形のの活性化関数に分類される。
- 定義
出力値は、\(x\) が小さいほど \(0\) になく近づき、\(x\) が大きいほど \(1\) に限りなく近づく。
\[
h(x) = \frac{1}{1+e^{-x}}
\]
- 実装
$ python
>>> import numpy as np
>>> import matplotlib.pylab as plt
>>> def sigmoid_func(x): # シグモイド関数の定義
... return 1 / (1 + np.exp(-x)) # 自然対数の低 (e) の -x 乗
...
- グラフ出力
$ python
>>> x = np.arange(-5.0, 5.0, 0.1) # 区間を-5~5 まで、描画制度を 0.1 刻みに設定
>>> y = sigmoid_func(x) # シグモイド関数をコール
>>> plt.title("sigmoid_func\n# arange:-5.0, 5.0, 0.1, xlabel:x, ylabel:y") # グラフタイトルを設定
Text(0.5, 1.0, 'sigmoid_func\n# arange:-5.0, 5.0, 0.1, xlabel:x, ylabel:y')
>>> plt.ylim(-0.1, 1.1) # y軸の範囲を設定
(-0.1, 1.1)
>>> plt.xlabel("x") # x軸のラベルを設定
Text(0.5, 0, 'x')
>>> plt.ylabel("y") # y軸のラベルを設定
Text(0, 0.5, 'y')
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x7f727fbc1be0>]
>>> plt.savefig('/var/www/vops/ops/macuos/static/macuos/img/pid18_2.png') # グラフの出力
ReLU関数
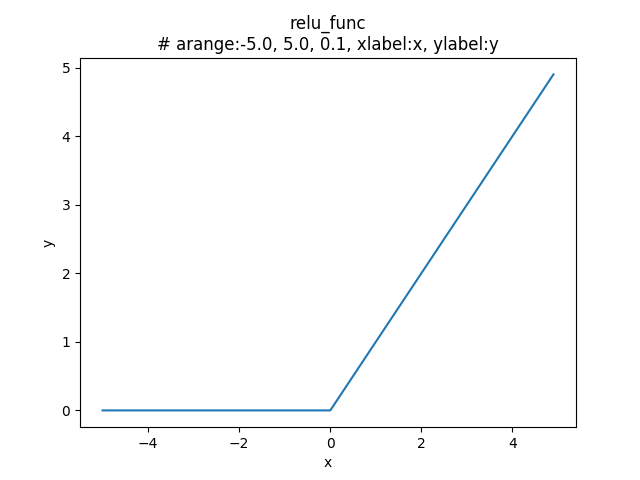
ReLU(Rectified Linear Unit:ランプ関数、正規化線形関数)と呼ばれ、非線形の活性化関数に分類される。
※ 最近では、ニューラルネットワークにおいて、シグモイド関数より、ReLU関数が多く用いられるようになった。
- 定義
\(x\) が \(0\) より大きい場合、\(x\) を出力し、\(0\) 以下である場合、\(0\) を出力する。
\[
{\normalsize
h(x) =
\begin{cases}
x \hspace{5pt}\text{if}\hspace{5pt}x > 0 \\
0 \hspace{5pt}\text{if}\hspace{5pt}x \leqq 0
\end{cases}
}
\]
- 実装
$ python
>>> import numpy as np
>>> import matplotlib.pylab as plt
>>> def relu_func(x): # ReLU関数の定義
... return np.maximum(0, x)
...
- グラフ出力
$ python
>>> x = np.arange(-5.0, 5.0, 0.1) # 区間を-5~5 まで、描画制度を 0.1 刻みに設定
>>> y = relu_func(x) # ReLU関数をコール
>>> plt.title("relu_func\n# arange:-5.0, 5.0, 0.1, xlabel:x, ylabel:y") # グラフタイトルを設定
Text(0.5, 1.0, 'relu_func\n# arange:-5.0, 5.0, 0.1, xlabel:x, ylabel:y')
>>> plt.xlabel("x") # x軸のラベルを設定
Text(0.5, 0, 'x')
>>> plt.ylabel("y") # y軸のラベルを設定
Text(0, 0.5, 'y')
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x7fbf1cfeecc0>]
>>> plt.savefig('/var/www/vops/ops/macuos/static/macuos/img/pid18_3.png')
>>>
恒等関数
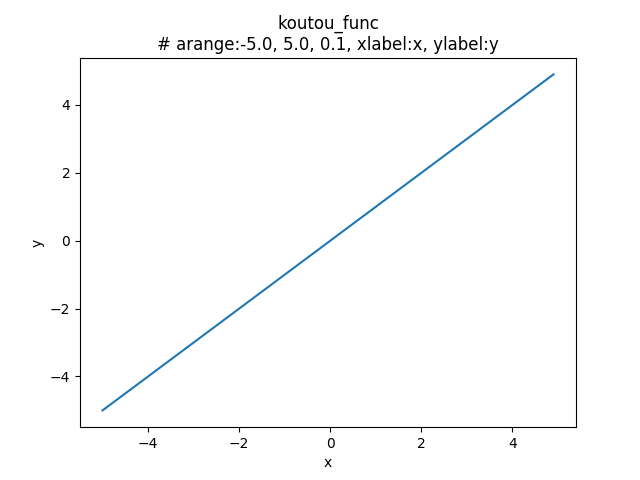
出力層で使われる線形の活性化関数に分類される。
- 定義
\(x\) をそのまま出力する。
\[
{\normalsize
h(x) = x
}
\]
- 実装
$ python
>>> import numpy as np
>>> import matplotlib.pylab as plt
>>> def koutou_func(x): # 恒等関数の定義
... return x
...
- グラフ出力
$ python
>>> x = np.arange(-5.0, 5.0, 0.1) # 区間を-5~5 まで、描画制度を 0.1 刻みに設定
>>> y = koutou_func(x) # 恒等関数をコール
>>> plt.title("koutou_func\n# arange:-5.0, 5.0, 0.1, xlabel:x, ylabel:y") # グラフタイトルを設定
Text(0.5, 1.0, 'koutou_func\n# arange:-5.0, 5.0, 0.1, xlabel:x, ylabel:y')
>>> plt.xlabel("x") # x軸のラベルを設定
Text(0.5, 0, 'x')
>>> plt.ylabel("y") # y軸のラベルを設定
Text(0, 0.5, 'y')
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x7fba4d928f60>]
>>> plt.savefig('/var/www/vops/ops/macuos/static/macuos/img/pid18_4.png')
>>>
ソフトマックス関数
分類問題で使われる非線形の活性化関数に分類される。
- 定義
\(n \leqq k\) の時、\(k\) 番目の出力 \(h(x_{k})\) を表す。
\[
{\normalsize
h(x_{k}) = \frac{e^{x_{k}}}{\sum_{i=1}^{n} e^{x_{i}}}
}
\]
- 実装
$ python
>>> def softmax_func(x): # ソフトマックス関数の定義
... exp_x = np.exp(x)
... sum_exp_x = np.sum(exp_x)
... y = exp_x / sum_exp_x
... return y
...
- グラフ出力
$ python
>>> x = np.arange(-5.0, 5.0, 0.1) # 区間を-5~5 まで、描画制度を 0.1 刻みに設定
>>> y = koutou_func(x) # ソフトマックス関数をコール
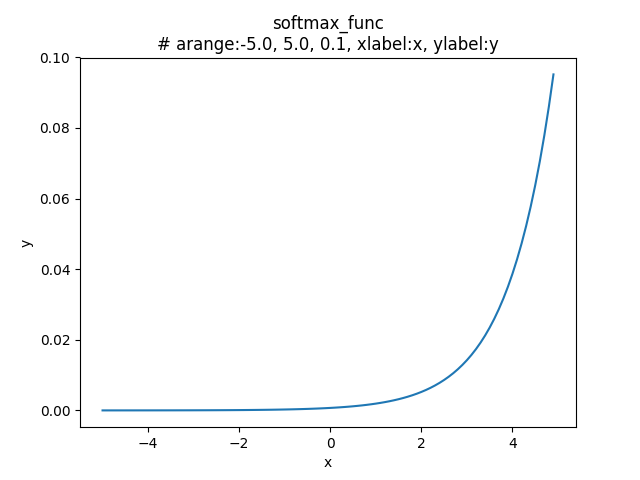
>>> plt.title("softmax_func\n# arange:-5.0, 5.0, 0.1, xlabel:x, ylabel:y") # グラフタイトルを設定
Text(0.5, 1.0, 'softmax_func\n# arange:-5.0, 5.0, 0.1, xlabel:x, ylabel:y')
>>> plt.xlabel("x") # x軸のラベルを設定
Text(0.5, 0, 'x')
>>> plt.ylabel("y") # y軸のラベルを設定
Text(0, 0.5, 'y')
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x7ff04a9c4d68>]
>>> plt.savefig('/var/www/vops/ops/macuos/static/macuos/img/pid18_5.png')
>>>
参考文献
- 斎藤 康毅(\(2018\))『ゼロから作るDeep Learning - Pythonで学ぶディープラーニングの理論と実装』株式会社オライリー・ジャパン